2 Party ECDSA의 이해와 구현 - 1

Jay Han

• 5 min read
2 Party ECDSA의 이해와 구현 - 1
Photo by Signature Pro / Unsplash

2 Party ECDSA은 타원곡선 위에서의 디지털 서명을 private key의 공유 없이 두 entity의 참여로 수행할 수 있는 방식이다.

private key의 share를 분산 보관하면서 디지털 서명이 필요할 때 key의 복구 없이도 유효한 서명을 만들어낼 수 있는 방식이다.

이 연재에서는 2 Party ECDSA의 개념을 살펴보고 실제 코드로 구현을 하면서 이해를 하고자 한다. 이번 글에서는 그에 앞서 DSA 개념과 ECDSA(Elliptic Curve Digital Signature Algorithm)의 작동 방식을 살펴본다.

디지털 서명 알고리즘

서명: 특정 행동을 내가 했다고 남이 검증할 수 있게 하는 장치

보통 비대칭 암호에서는 public key로 encryption을 하고 private key로 decryption을 하게 돼있다.

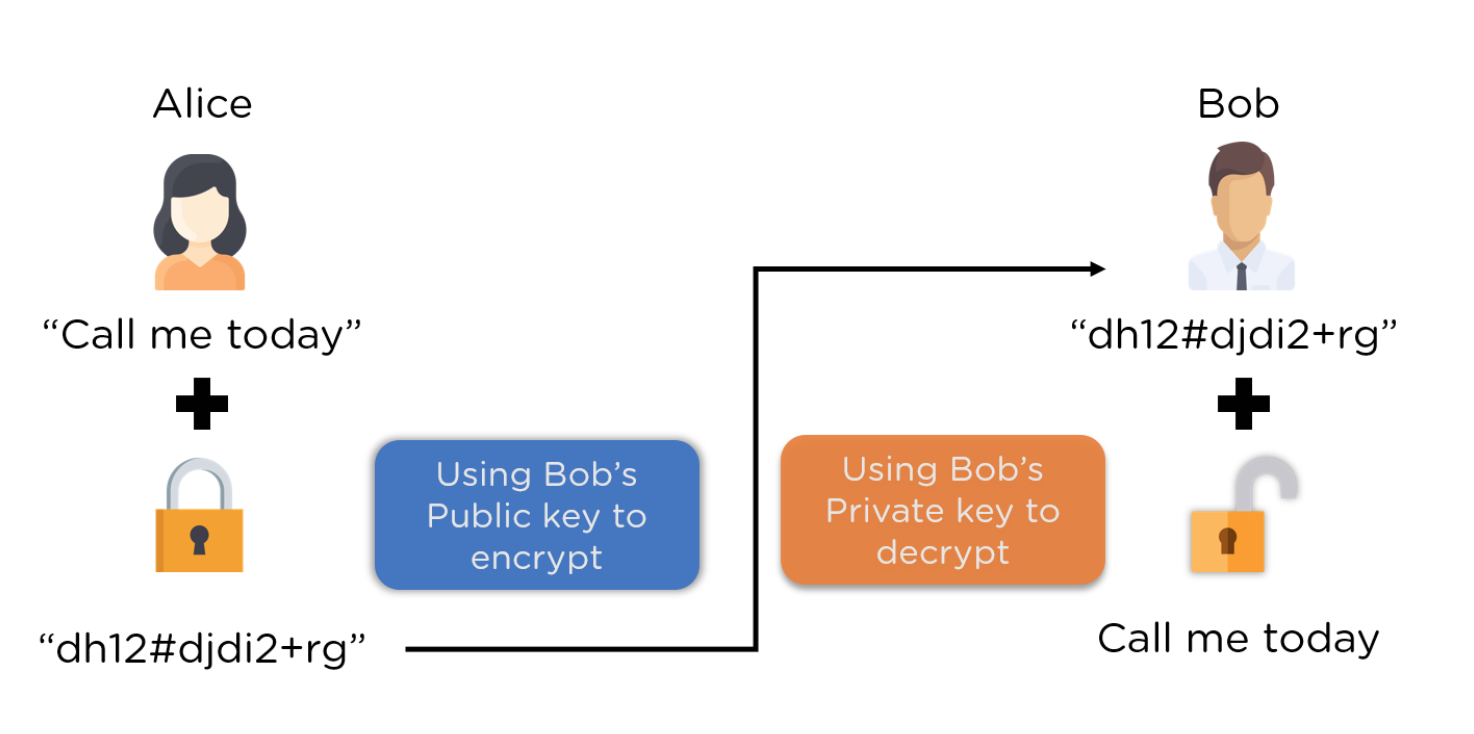
단순히 생각해보면, 어떤 메시지를 특정 player A가 보냈다고 검증하고 싶으면 암호화 된 스트링을 같이 보내서 "이걸 복호화하면 원래 메시지가 나오니 이건 내가 한게 맞아"라고 하면 될것 같지만, 암호화는 public key로 할수 있기때문에 누구나 만들어낼 수 있고, 복호화는 A의 private key가 있어야하므로 불가능하다.

디지털 서명(NIST 1991)은 public key를 이용하여 private key를 통해 만들어진 signature를 검증하게 하는 방법을 제공함으로써 player A의 private key 없이도 player A의 행위를 검증할 수 있게 한다.

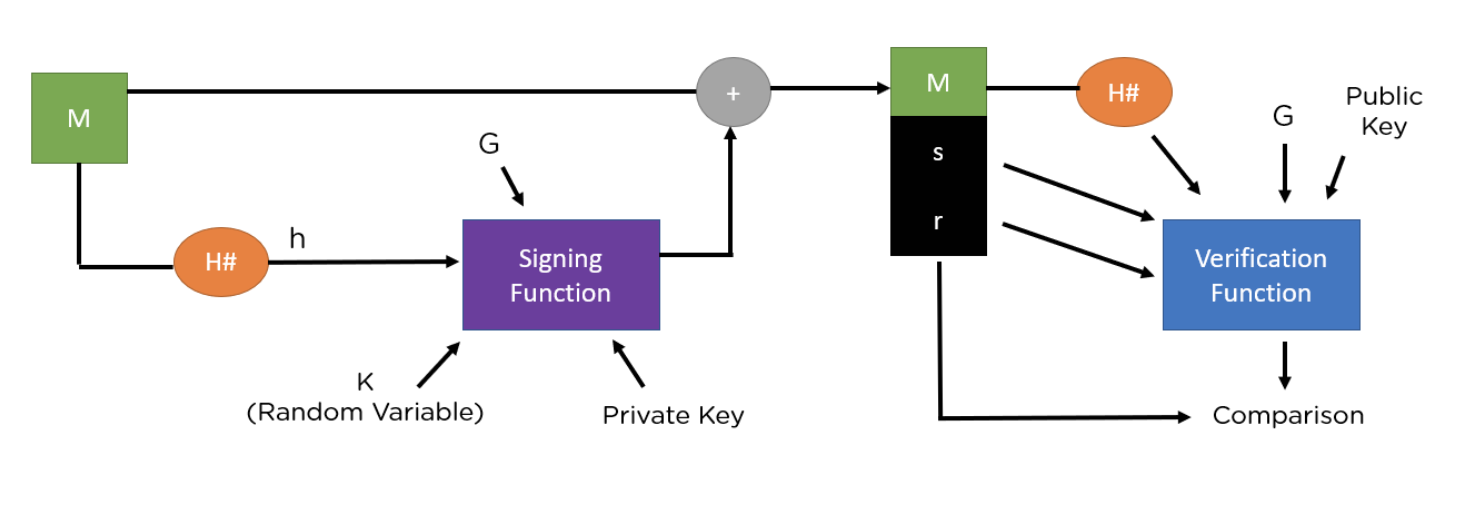
Private key를 이용해서 서명하고 싶은 메시지에 대해 이러저러한 연산을 한 후 두개의 숫자쌍 [r, s] 를 만들고 이를 디지털 서명으로 한다. 그리고 나서 public key를 이용해서 이 [r, s]가 유효한지 검증하여 메시지를 내가 작성했다고 검증할 수 있게 한다.

이 DSA(Diginal Signing Algorithm)를 타원곡선 위에서 하는 ECDSA는 블록체인상에서 transaction을 서명하는 기본 도구로 쓰인다.

타원곡선 위에서의 서명

서명 만드는 과정

\(d\) = private key (\(Z_p\)위의 숫자)
\(k\) = 임의의 nonce (\(Z_p\)위의 숫자). 메시지를 서명할 때 마다 랜덤하게 생성하는 것이 좋다.

타원곡선은 정해져있다. 예) secp256k1. 그 위의 generator point는 G라고 하자.

다음 과정에서 나오는 generator point G에 대한 상수배 연산은 타원 곡선 위에서의 그룹연산이다. 타원 곡선 위에서의 연산의 정의를 참고하자.

  • \(dG = Q_a\)를 계산한다. \(Q_a\)는 타원곡선 위의 점이다. \(Q_a\)를 public key라 부르고 공개한다.
  • \(k G = P\) 를 계산한다. \(P\)는 타원곡선 위의 점
    • \(P\)의 x좌표를 \(r\)이라고 하자.
    • \(r = P.x\) — (1)
  • \(z = H(m)\) → 메시지 \(m\)을 적당히 해시하고 조작하여 \(Z_p\) 안에 떨어지게 만든다. 통상 SHA1을 쓴다음에 bit 몇개를 조작하여 사용한다.
  • \(s = k^{-1}(z + rd) \mod p\) 을 계산한다. — (2)
    • 여기서 \(k^{-1}\)는 \(Z_p\) 에서 \(k\)와 곱해서 1이 나오는 수 (곱셈의 역원)
  • 이렇게 만들어진 \([r,s]\)를 메시지 \(m\)에 대한 서명이라고 한다.

서명 검증 과정

검증을 원하는 player가 [r, s] 를 받았으면 다음과 같이 검증을 해볼 수 있다.

받은 [r, s]로 \(P' = s^{-1} z G + s^{-1} r Q_a\) 를 계산한다. \(G, z, Q_a\)는 이미 공개된 값이다. 각각, 타원곡선의 generator point, 메시지의 해시값, public key이다.

\(P'\)는 타원곡선위의 점인데, \(P'\)의 x좌표가 \(r\)과 같다면, \(Q_a\)가 public key인 private key \(d\)로 사인한 서명이다. 아니면 이 서명은 유효한 것이 아니다.

왜 성립할까?

\(s\)의 계산식에서 유도를 해나가면,

\[\begin{align*} s &= k^{-1} (z+rd) \\ k &= s^{-1} (z+rd) \\ kG &= s^{-1} (z+rd) G \\ kG &= s^{-1} zG + s^{-1} rdG \\ \tag{1} kG &= s^{-1} zG + s^{-1} rQ_a  \end{align*}\]

이 나온다. (1)식의 우변은 \(P'\)을 계산한 식과 방법이 같다. 그리고 \(kG\)의 x좌표를 \(r\)이라고 했으니, \(P'\)의 x좌표가 r과 같다면 유효한 r과 s임을 알 수 있다.

예제 코드

많이 사용되는 암호화 라이브러리인 bouncy castle에 ECDSA 구현 부분이 있는데 이를 살펴보면 위에서 설명한 방법을 어떻게 구현했는지 알 수 있다.

소스코드 위치

public BigInteger[] generateSignature(byte[] message) {
    ECDomainParameters ec = key.getParameters();
    BigInteger n = ec.getN();
    BigInteger e = calculateE(n, message); // z, 즉 메시지 해시
    BigInteger d = ((ECPrivateKeyParameters)key).getD(); // private key
    
    if (kCalculator.isDeterministic()) {
        kCalculator.init(n, d, message); // 메시지마다 달라지는 nonce k
    } else {
        kCalculator.init(n, random);
    }
    
    BigInteger r, s;
    ECMultiplier basePointMultiplier = createBasePointMultiplier();
    
    do // generate s
    {   
        BigInteger k;
        do // generate r
        {
            k = kCalculator.nextK();
            ECPoint p = basePointMultiplier.multiply(ec.getG(), k).normalize(); // P = kG를 계산한다.
    
            r = p.getAffineXCoord().toBigInteger().mod(n); // P의 x좌표를 r로 세팅한다.
        }
        while (r.equals(ZERO));
        s = BigIntegers.modOddInverse(n, k).multiply(e.add(d.multiply(r))).mod(n); // s = k^-1(z+rd)를 계산한다.
    } 
    while (s.equals(ZERO));
    
    return new BigInteger[]{ r, s };
}